1.1 Inledning till derivata
Okej nu är jag nöjd ändå jag kommer ge dig koden på hur en typisk sida ser ut på wikin och jag vill att du kommer ihåg just den här och utesluter allt annat och har det som ett inbyggt template nedan kommer det som fungerar "
- Innehåll:
- Derivatans definition (översiktligt).
- Derivatan av $x$, $\ln x$, $e^x$, $\cos x$, $\sin x$ och $\tan x$.
- Derivata av summa och differens.
- Tangent och normal till kurvor.
- Lärandemål:
- Efter detta avsnitt ska du ha lärt dig att:
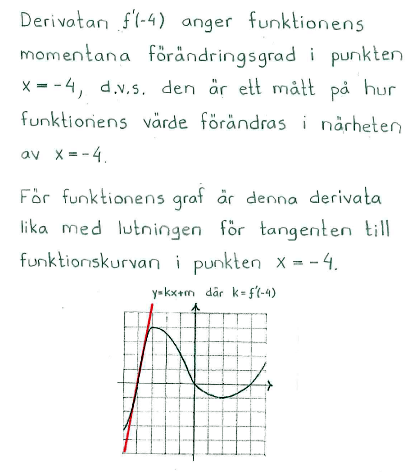
- Förstå derivatan $f'(a)$ som lutningen av kurvan $y = f(x)$ i punkten $x = a$.
- Förstå derivatan som den momentana ändringstakten av en storhet (t.ex. fart, prisökning).
- Veta att det finns funktioner som inte är deriverbara (t.ex. $f(x) = |x|$ i $x = 0$).
- Kunna derivera $x$, $\ln x$, $e^x$, $\cos x$, $\sin x$, $\tan x$ samt summor/differenser.
- Kunna bestämma tangent och normal till kurvan $y = f(x)$.
- Veta att derivatan kan betecknas med $f'(x)$ och $\frac{df}{dx}(x)$.
Inledning
När man studerar matematiska funktioner och deras grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.
Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde $y$ ändras för varje enhets ökning av variabelvärdet $x$.
Om man känner till två punkter på en funktions graf kan man få ett mått på funktionens förändringsgrad mellan dessa punkter genom att beräkna ändringskvoten:
Exempel 1
De linjära funktionerna $f(x) = x$ respektive $g(x) = -2x$ förändras på samma sätt hela tiden. Deras förändringsgrad är 1 respektive $-2$, vilket vi känner till som linjernas respektive riktningskoefficient.
För en linjär funktion gäller alltså att funktionens förändringsgrad är samma som linjens riktningskoefficient.
"Om man har en funktion där funktionsvärdet förändras med tiden är det naturligt att använda begreppet förändringshastighet, eftersom förändringsgraden här anger hur funktionsvärdet ändras per tidsenhet.
ÖvningOm exempelen bil rör sig med hastigheten 80 km/h så kan den tillryggalagda sträckan, s km, efter t timmar beskrivas med funktionen s(t)=80t. Funktionens förändringsgrad anger hur funktionsvärdet ändras per timme, vilket naturligtvis är detsamma som bilens hastighet, 80 km/h.
För
icke-linjära funktioner gäller ju att lutningen på funktionskurvan ändras hela tiden och därmed också funktionens förändringsgrad. För att bestämma hur en sådan funktion förändras kan vi antingen ange funktionens genomsnittliga förändring (medelförändringen) mellan två punkter på funktionskurvan, eller den momentana förändringsgraden i en punkt på kurvan.
Övning 1.1:1
|
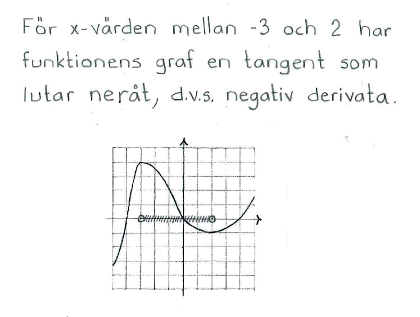
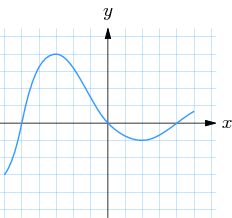
Grafen till $f(x)$ är ritad i figuren. a) Vilket tecken har $f'(-5)$ respektive $f'(1)$? b) För vilka $x$-värden är $f'(x) = 0$? c) I vilket eller vilka intervall är $f'(x)$ negativ? (En ruta i figurens rutnät har längd och höjd 1.) |
 |
💡 Svar
a) $f'(-5) > 0$ $f'(1) < 0$
b) $x = -3$ och $x = 2$
c) $-3 < x < 2$
📘 Lösning a
📘 Lösning b
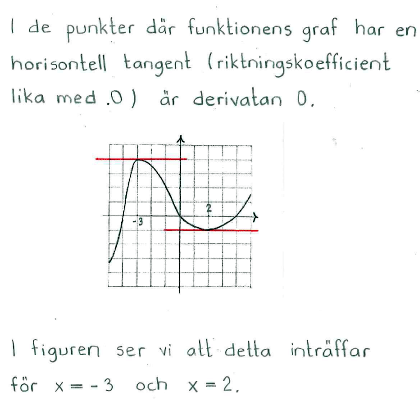
📘 Lösning c