1.1 Inledning till derivata
- Innehåll:
- Derivatans definition (översiktligt).
- Derivatan av $x$, $\ln x$, $e^x$, $\cos x$, $\sin x$ och $\tan x$.
- Derivata av summa och differens.
- Tangent och normal till kurvor.
- Lärandemål:
- Efter detta avsnitt ska du ha lärt dig att:
- Förstå derivatan $f'(a)$ som lutningen av kurvan $y = f(x)$ i punkten $x = a$.
- Förstå derivatan som den momentana ändringstakten av en storhet (t.ex. fart, prisökning).
- Veta att det finns funktioner som inte är deriverbara (t.ex. $f(x) = |x|$ i $x = 0$).
- Kunna derivera $x$, $\ln x$, $e^x$, $\cos x$, $\sin x$, $\tan x$ samt summor/differenser.
- Kunna bestämma tangent och normal till kurvan $y = f(x)$.
- Veta att derivatan kan betecknas med $f'(x)$ och $\frac{df}{dx}(x)$.
Inledning
När man studerar matematiska funktioner och deras grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.
Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde $y$ ändras för varje enhets ökning av variabelvärdet $x$.
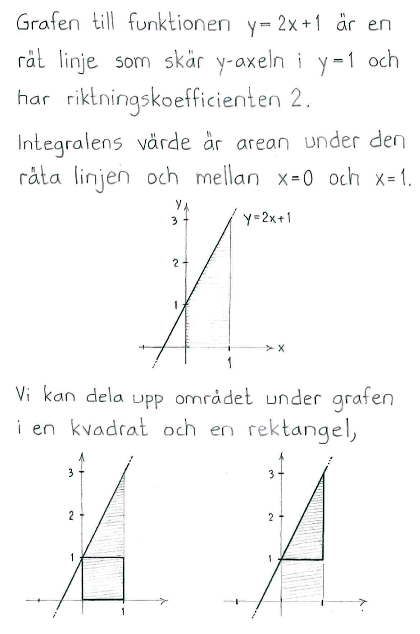
Om man känner till två punkter på en funktions graf kan man få ett mått på funktionens förändringsgrad mellan dessa punkter genom att beräkna ändringskvoten:
Exempel 1
De linjära funktionerna $f(x) = x$ respektive $g(x) = -2x$ förändras på samma sätt hela tiden. Deras förändringsgrad är 1 resp.respektive –2, vilket vi känner till som linjernas respektive riktningskoefficient.
Grafen till $f(x) = x$ har riktningskoefficient 1.
Grafen till $g(x) = -2x$ har riktningskoefficient $-2$.
För en linjär funktion gäller alltså att funktionens förändringsgrad är samma som linjens riktningskoefficient.