New Page
## 2.1 Övningar ### Övning 2.1:1 **Tolka integralerna som areor och bestäm deras värde** **a)** $$\int_{-1}^{2} 2 \, dx$$ **b)** $$\int_{0}^{1} (2x + 1) \, dx$$ **c)** $$\int_{0}^{2} (3 - 2x) \, dx$$ **d)** $$\int_{-1}^{2} |x| \, dx$$ --- ### 📌 Svar (klicka för att visa)
Visa svar a
$$\int_{-1}^{2} 2 \, dx = 2 \cdot (2 - (-1)) = 2 \cdot 3 = \boxed{6}$$
Visa svar b
$$ \int_{0}^{1} (2x + 1) \, dx = \left[ x^2 + x \right]_0^1 = (1 + 1) - 0 = \boxed{2} $$
Visa svar c
$$ \int_{0}^{2} (3 - 2x) \, dx = \left[ 3x - x^2 \right]_0^2 = (6 - 4) - 0 = \boxed{2} $$
Visa svar d
Dela upp absolutbeloppet: $$ \int_{-1}^{0} -x \, dx + \int_{0}^{2} x \, dx = \left[ -\frac{x^2}{2} \right]_{-1}^{0} + \left[ \frac{x^2}{2} \right]_0^2 $$ $$ = \left(0 - (-\frac{1}{2})\right) + \left(\frac{4}{2} - 0\right) = \frac{1}{2} + 2 = \boxed{\frac{5}{2}} $$
### b) $$\int_{0}^{1} (2x + 1) \, dx$$
Visa svar b
**Svar:** $$\int_{0}^{1} (2x + 1) \, dx = [x^2 + x]_0^1 = 1 + 1 = \boxed{2}$$ 📷 **Visualisering:**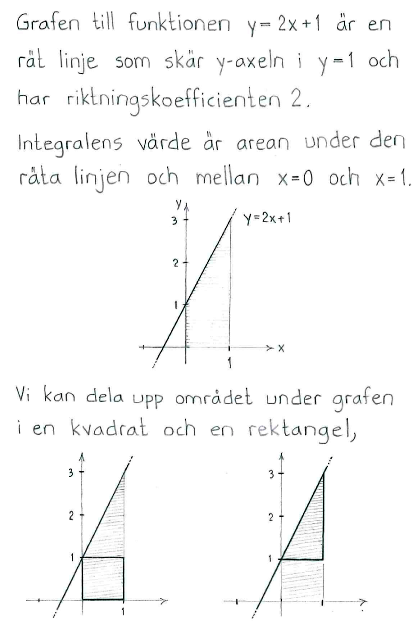 
b)
$$\int_{0}^{1} (2x + 1) \, dx$$
Visa svar b
Svar:
$$\int_{0}^{1} (2x + 1) \, dx = [x^2 + x]_0^1 = 1 + 1 = \boxed{2}$$
Visualisering:
